字符串匹配之 KMP 算法

1 问题描述^[1]

给你两个字符串 text 和 pattern ，请你在 text 字符串中找出 pattern 字符串的第一个匹配项的下标（下标从 0 开始）。如果 pattern 不是 text 的一部分，则返回 -1 。

其中 1 <= pattern.length, text.length <= 10^4 。

2 Solution: Brute Force Search

def brute_force_search(text, pattern):
    text_len = len(text)
    pattern_len = len(pattern)

    for i in range(text_len - pattern_len + 1):
        match = True
        for j in range(pattern_len):
            if text[i + j] != pattern[j]:
                match = False
                break

        if match:
            return i

    return -1

该朴素算法（brute-force）字符串搜索的时间复杂度为 O((n - m + 1) * m) ，其中 n 是文本的长度，m 是 pattern 的长度。

具体分析如下：

外层循环从 i = 0 到 i = n - m ，总共 (n - m + 1) 次迭代。
对于外层循环的每次迭代，内层循环运行 m 次，其中m是 pattern 的长度。
在内层循环中，对于 pattern 的每个字符，执行了常数时间的比较。

因此，总体时间复杂度为 O((n - m + 1) * m) ，其中 (n - m + 1) 表示文本中 pattern 可能开始的位置数量，m 是 pattern 的长度。

该算法的空间复杂度为 O(1) ，因为它使用了常数额外空间，与输入大小无关。

3 Solution: KMP Algorithm

3.1 Basic idea

当匹配过程中发生 Mismatch 时

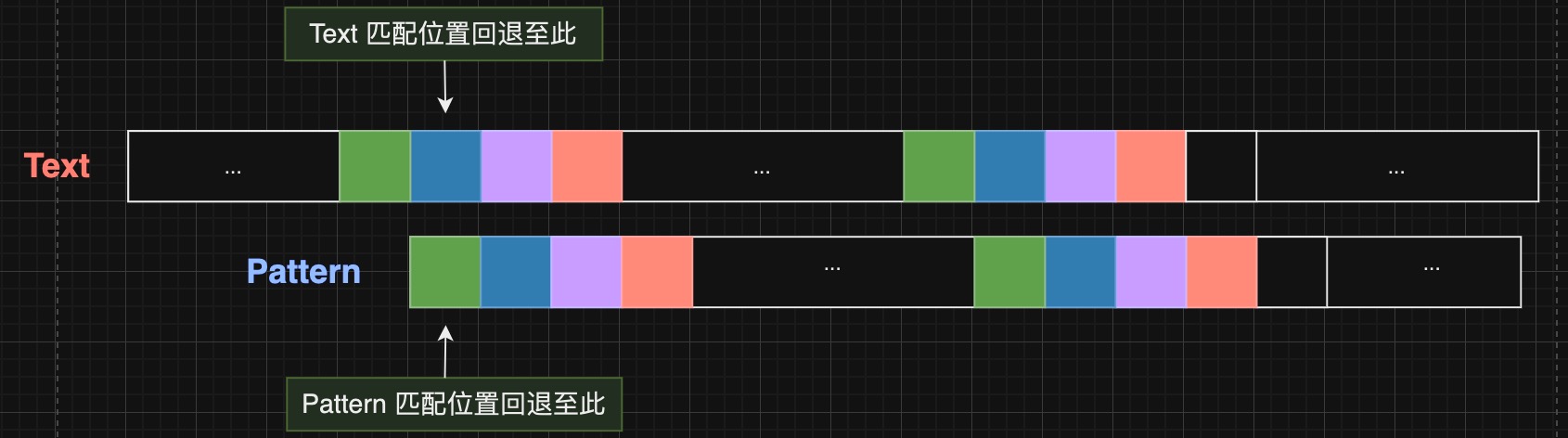
Brute Force Search 算法:

text 匹配位置回退到下一个起始匹配位置
pattern 匹配位置回退到0

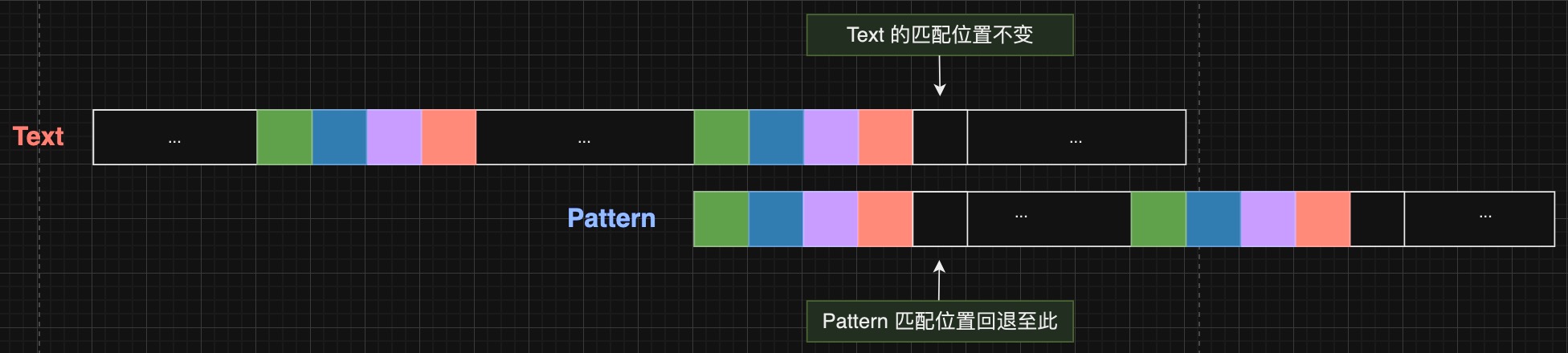
KMP 算法:

text 的匹配位置永远不会回退
pattern 的匹配位置会根据当前 Mismatch 位置的最长严格公共前后缀（LPS）信息回退

因此在搜索前，需要预先计算出 pattern 每个位置处的 LPS 信息，即在各个位置 Mismatch 时，pattern 匹配位置需要回退到哪里。

3.2 LPS 具体解释

在 KMP 算法中，LPS 代表 “Longest Proper Prefix which is also Suffix” ，即最长的既是 Proper（严格）前缀又是后缀的字符串。

具体解释如下：

Prefix: 一个字符串的前缀是指从字符串的开头开始的任何子串，包括空字符串和字符串本身。对于字符串 "ABC" ，它的前缀字符串包括： "" , "A" , "AB" , "ABC"。
Proper Prefix: 是指一个字符串的严格前缀，即不包括字符串本身的前缀。对于字符串 "ABC" ，其proper prefix包括： "" , "A" , "AB"。
Suffix: 一个字符串的后缀是指从字符串的结尾开始的任何子串，包括空字符串和字符串本身。对于字符串 "ABC" ，它的后缀包括："" , "C" , "BC" , "ABC"。

因此，字符串 "ABAB" 的 LPS 是 "AB"，字符串 "ABC" 的 LPS 是 ""。

3.3 算法预处理：为 pattern 构建 LPS 数组

LPS 数组是一个用于加速 KMP 算法的辅助数组，用于在匹配失败时跳过尽可能多的字符，从而提高字符串匹配的效率。

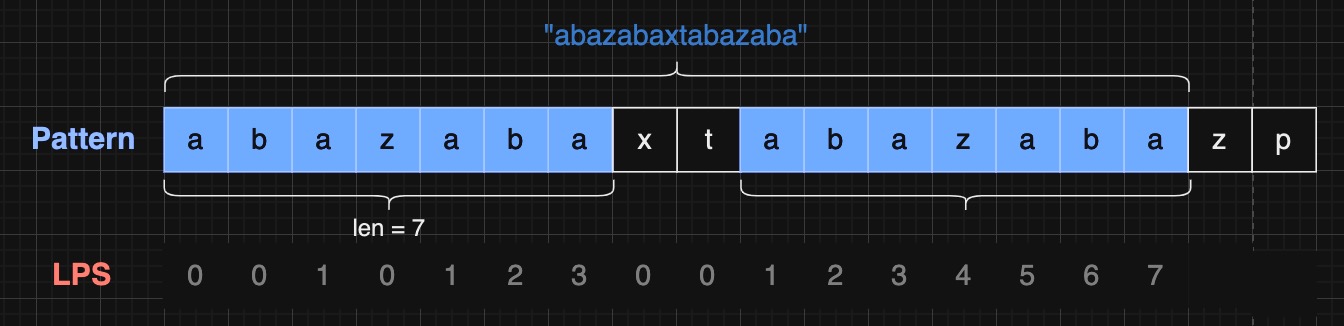
例如，对于 pattern "abazabaxtabazabazp" , LPS 数组是 [0, 0, 1, 0, 1, 2, 3, 0, 0, 1, 2, 3, 4, 5, 6, 7, 4, 0]。

LPS[i] 含义：字符串 pattern[:i+1] 的 LPS 的长度

"a": 公共严格前后缀为"" 或者说 无公共严格前后缀, LPS[0] 永远等于0

"ab": 无公共严格前后缀，LPS[1] = 0

"aba": 公共严格前后缀为 "a"，LPS[2] = 1

"abaz": 无公共严格前后缀，LPS[3] = 0

"abaza": 公共严格前后缀为 "a"，LPS[4] = 1

"abazab": 公共严格前后缀为 "ab"，LPS[5] = 2

"abazaba": 公共严格前后缀为 "aba"，LPS[6] = 3

"abazabax": 无公共严格前后缀，LPS[7] = 0

"abazabaxt": 无公共严格前后缀，LPS[8] = 0

"abazabaxta": 公共严格前后缀为 "a"，LPS[9] = 1

"abazabaxtab": 公共严格前后缀为 "ab"，LPS[10] = 2

"abazabaxtaba": 公共严格前后缀为 "aba"，LPS[11] = 3

"abazabaxtabaz": 公共严格前后缀为 "abaz"，LPS[12] = 4

"abazabaxtabaza": 公共严格前后缀为 "abaza"，LPS[13] = 5

"abazabaxtabazab": 公共严格前后缀为 "abazab"，LPS[14] = 6

"abazabaxtabazaba": 公共严格前后缀为 "abazaba"，LPS[15] = 7

"abazabaxtabazabaz": 公共严格前后缀为 "abazabaz"，LPS[16] = 4

"abazabaxtabazabazp": 无公共严格前后缀，LPS[17] = 0

如何使用代码来生成 LPS 数组呢？

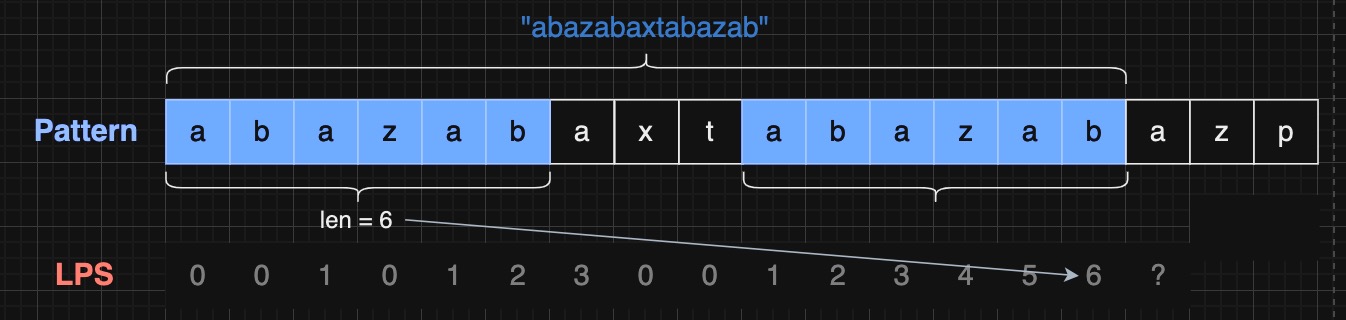
假设我们已经计算出了 "abazabaxtabazab" 的 LPS 为 "abazab"

如何计算 "abazabaxtabazaba" 的 LPS 呢？

显然 pattern[6] == pattern[15]

"abazabaxtabazaba" 的 LPS 为 "abazaba"

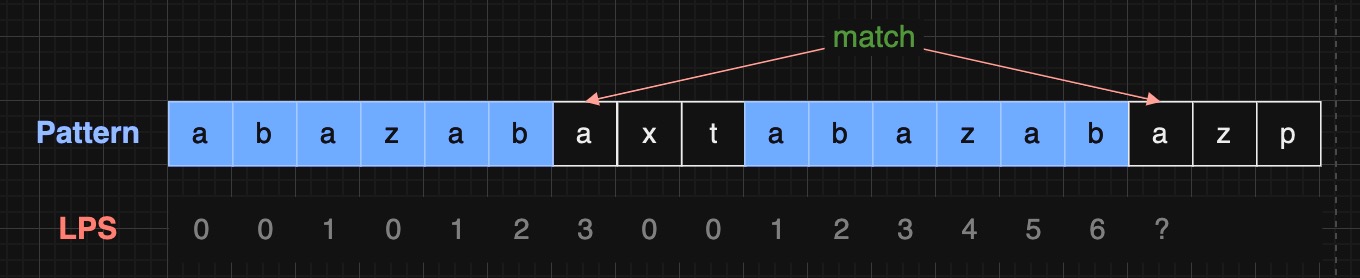
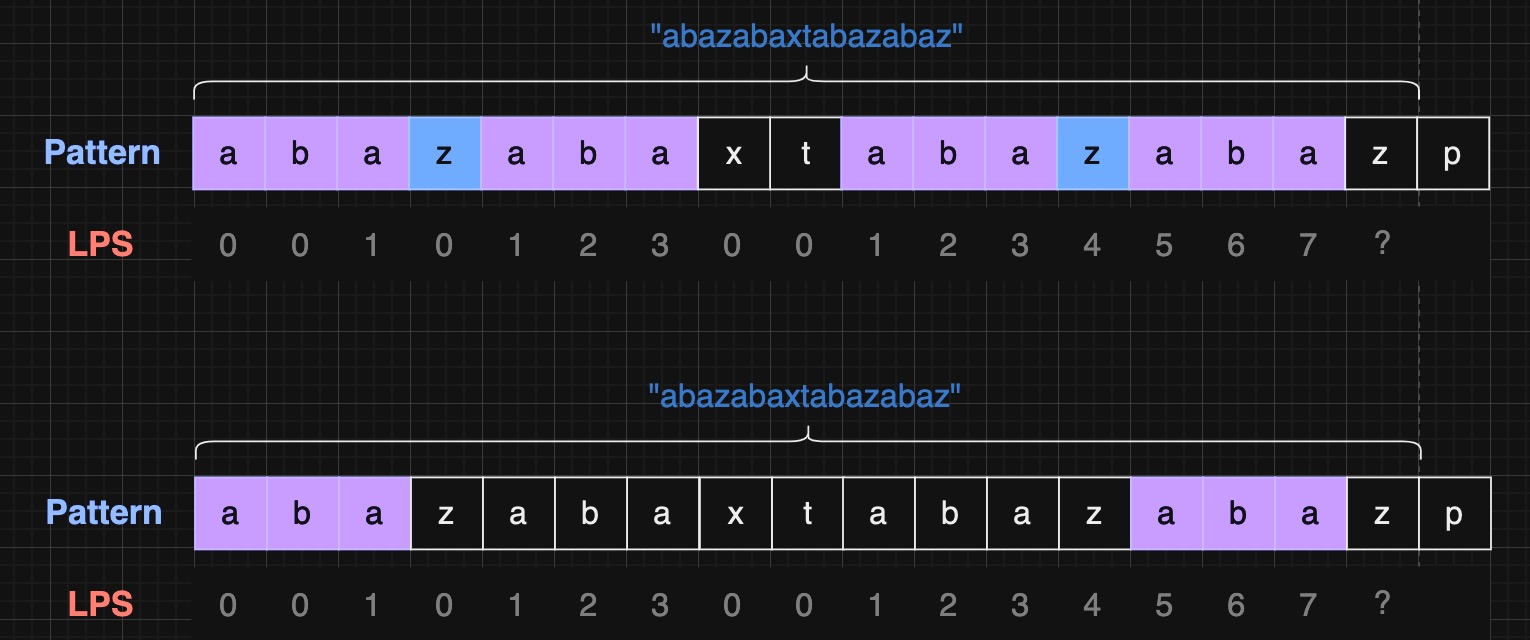
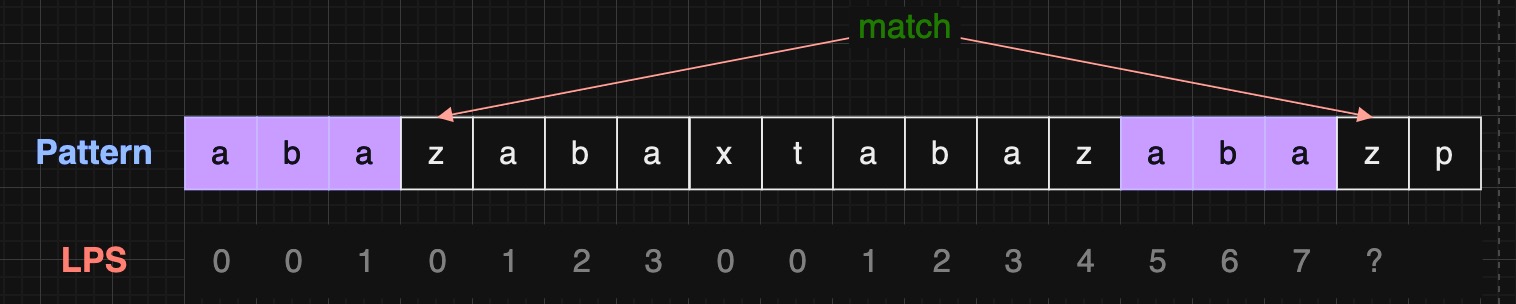
接下来计算 "abazabaxtabazabaz" 的 LPS

此刻 pattern[7] != pattern[16]

我们需要找到一个更短的前缀进行尝试

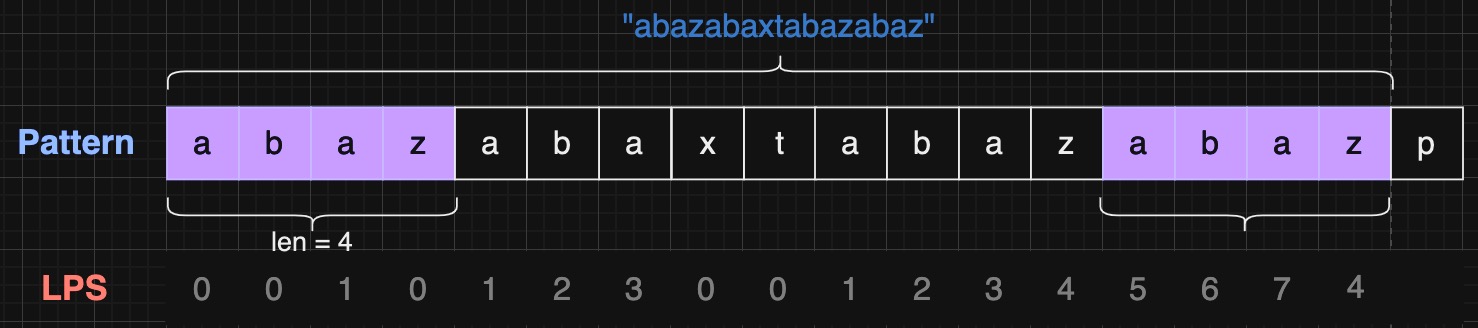
此刻 pattern[4] == pattern[16]

"abazabaxtabazabaz" 的 LPS 为 "abaz"

最后计算 "abazabaxtabazabazp" 的 LPS

发现没有更短前缀可以尝试(或者说这里在匹配 "" 前缀)，并且 pattern[0] != pattern[17] ，所以 LPS = 0

当没有前缀可以匹配(或者说在匹配 "" 前缀)时的两种情况

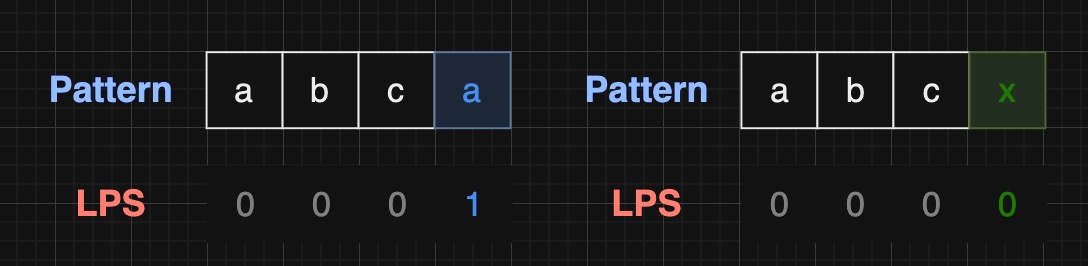
当前匹配字符与 pattern[0] 相等，LPS = 1
当前匹配字符与 pattern[0] 不相等，LPS = 0

实现逻辑总结：

我们在最开始初始化一个前缀长度变量 prefix = 0 ，表示只有单个字符的字符串没有 LPS 。
然后从 i = 1 开始由短到长逐渐计算每个字符串的 LPS

匹配成功时的增长： 如果字符匹配成功（pattern[i] == pattern[prefix]），则继续增加前缀的长度（prefix += 1）。

匹配失败时的回退： 当发生匹配失败时（pattern[i] != pattern[prefix]），通过回退的方式，找到一个更短的前缀进行尝试。

def compute_lps_array(pattern: str) -> list[int]:
    lps = [0] * len(pattern)

    # 初始前缀长度为0
    prefix = 0

    # 从第二个字符开始遍历pattern
    for i in range(1, len(pattern)):
        # 匹配失败时，回退前缀长度，条件 prefix > 0 保证了可回退 
        while prefix > 0 and pattern[i] != pattern[prefix]:
            prefix = lps[prefix - 1]

        # 匹配成功，增加前缀长度
        if pattern[i] == pattern[prefix]:
            prefix += 1
        
        # 匹配失败时 lps[i] = 0
        lps[i] = prefix
    
    return lps

时间复杂度分析

初始时我觉得代码包括两层循环结构，所以时间复杂度是 O(m^2) ，其中 m 是 pattern 的长度，但是网上都说是 O(m) 让我很难理解。

在每一轮 for 循环中，prefix 在匹配成功时增加1，而在匹配失败时可能经过多次回退。然而，总的回退次数受限于总的成功匹配次数，prefix 至多增加到 m，所以总的回退次数至多也是 m。因此，整体的时间复杂度为 O(m)。

可以这样想，我有一张初始余额为0 (prefix = 0)的银行卡，每次匹配成功，就在卡里存1块钱(prefix += 1)，每次匹配失败时，就花一次钱(prefix = lps[prefix - 1])，但是花钱的额度不能超过余额(同时是正整数元）。

在整个构建 lps[] 的过程中，我至多存 m 块钱，因此我至多消费 m 块钱，所以消费次数(匹配失败回退次数)一定不超过 m。

# 回退虽然在两层循环中进行，但是整个过程至多回退m次
for i in range(1, len(pattern)):
    while prefix > 0 and pattern[i] != pattern[prefix]:
        prefix = lps[prefix - 1]
    
    # ...

打破了我对嵌套的两层循环，一定是平方时间复杂度的认知。下面的这个例子，时间复杂度是 O(nlogn)

// 外层循环n次，内层循环log(n)次
for (int i = 0; i < n; i++) {
  for (int j = 1; j < n; j *= 2) {
    // 做一些操作
  }
}

3.4 搜索部分

def kmp_search(text: str, pattern: str) -> int:
    lps = compute_lps_array(pattern)
    text_index = pattern_index = 0
    
    while text_index < len(text):
        # 如果当前字符匹配，则继续比较下一个字符
        if text[text_index] == pattern[pattern_index]:
            text_index += 1
            pattern_index += 1
            
            # 如果pattern的所有字符都匹配，则返回匹配的起始索引
            if pattern_index == len(pattern):
                return text_index - len(pattern)
        # 如果当前字符不匹配，并且pattern的索引不是0，则回退到上一个匹配字符的位置
        elif pattern_index != 0:
            pattern_index = lps[pattern_index - 1]
        else:
            # 如果当前字符不匹配，并且pattern的索引已经是0，继续检查text的下一个字符
            text_index += 1
    
    return -1

搜索部分的时间复杂度为 O(n)，其中 n 为 text 的长度。

分析同上，pattern_index 在匹配成功时增加1，在匹配失败时回退。然而，总的回退次数受限于总的成功匹配次数，pattern_index 至多增加 n 次，所以总的回退次数至多也是 n。因此，整体的时间复杂度为 O(n)。

所以 KMP 算法的总体时间复杂度为 O(m + n)。

4 效率对比

起因是我想知道自己实现的 KMP 算法与 Python 自带的 str.find() 方法有多大的差距。

测试代码：

import time
import sys

def brute_force_search(text, pattern):
    text_len = len(text)
    pattern_len = len(pattern)

    for i in range(text_len - pattern_len + 1):
        match = True
        for j in range(pattern_len):
            if text[i + j] != pattern[j]:
                match = False
                break
        if match:
            return i

    return -1

def compute_lps_array(pattern: str) -> list[int]:
    lps = [0] * len(pattern)

    # 初始前缀长度为0
    prefix = 0

    # 从第二个字符开始遍历pattern
    for i in range(1, len(pattern)):
        # 匹配失败时，回退前缀长度，条件 prefix > 0 保证了可回退 
        while prefix > 0 and pattern[i] != pattern[prefix]:
            prefix = lps[prefix - 1]

        # 匹配成功，增加前缀长度（包括了 prefix = 0 且 匹配成功的情况）
        if pattern[i] == pattern[prefix]:
            prefix += 1
        
        # 匹配失败时 lps[i] = 0
        lps[i] = prefix
    
    return lps

def kmp_search(text: str, pattern: str) -> int:
    lps = compute_lps_array(pattern)
    text_index = pattern_index = 0
    
    while text_index < len(text):
        # 如果当前字符匹配，则继续比较下一个字符
        if text[text_index] == pattern[pattern_index]:
            text_index += 1
            pattern_index += 1
            
            # 如果pattern的所有字符都匹配，则返回匹配的起始索引
            if pattern_index == len(pattern):
                return text_index - len(pattern)
        # 如果当前字符不匹配，并且pattern的索引不是0，则回退到上一个匹配字符的位置
        elif pattern_index != 0:
            pattern_index = lps[pattern_index - 1]
        else:
            # 如果当前字符不匹配，并且pattern的索引已经是0，继续检查text的下一个字符
            text_index += 1
    
    return -1

# 创建文本和模式
text = 'a' * 1000000 + 'b'
pattern = 'a' * 100 + 'b'

# 测试暴力搜索算法
start = time.time()
res = brute_force_search(text, pattern)
end = time.time()
print('Brute Force Search:', (end - start) * 1000, 'ms, res =', res)

# 测试KMP算法
start = time.time()
res = kmp_search(text, pattern)
end = time.time()
print('KMP Search:', (end - start) * 1000, 'ms, res =', res)

# Python find()
start = time.time()
res = text.find(pattern)
end = time.time()
print('Python find:', (end - start) * 1000, 'ms, res =', res)

# output
# Brute Force Search: 10057.930946350098 ms, res = 999900
# KMP Search: 449.2683410644531 ms, res = 999900
# Python find: 1.7478466033935547 ms, res = 999900

最开始很震惊，为什么 Python str.find() 方法运行效率比我的 KMP 快这么多？

Python 自带的 find 方法是用 C 语言实现的，在底层经过高度优化，因此在大多数情况下会比纯 Python 代码更快。

而 KMP 算法虽然在某些情况下比朴素的字符串匹配算法更高效，但是它的实现依然是纯 Python 代码。尽管 KMP 算法的时间复杂度为 O(n + m)，其中 n 为文本长度，m 为模式串长度，但是在实际情况下，算法中涉及了大量的数组操作和条件判断，这些操作在 Python 中相比 C 语言而言速度会慢一些。因此，对于较大规模的数据，Python 自带的 find 方法通常会更快，因为它是直接调用底层 C 代码执行查找操作。

总的来说，Python 的内置方法通常会经过高度优化，运行速度更快，但在一些特定情况下，使用自定义的算法可能会更适合。

下面使用 C 来实现 KMP 算法看一下运行效率。

5 C语言版本KMP

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>

int kmp_search(const char* text, const char* pattern) {
    int tlen = 0;
    while (text[tlen] != '\0') {
        tlen++;
    }

    int plen = 0;
    while (pattern[plen] != '\0') {
        plen++;
    }

    int* lps = (int*)malloc(plen * sizeof(int));
    if (lps == NULL) {
        return -1; // 内存分配失败
    }

    // 构建 lps 数组
    int prefix = 0;
    for (int i = 1; i < plen; i++) {
        while (prefix > 0 && pattern[i] != pattern[prefix]) {
            prefix = lps[prefix - 1];
        }

        if (pattern[i] == pattern[prefix]) {
            prefix++;
        }

        lps[i] = prefix;
    }

    // 匹配过程
    int pi = 0;
    for (int ti = 0; ti < tlen; ti++) {
        while (pi > 0 && text[ti] != pattern[pi]) {
            pi = lps[pi - 1];
        }

        if (text[ti] == pattern[pi]) {
            if (pi == plen - 1) {
                free(lps);
                return ti - plen + 1;
            }
            pi++;
        }
    }

    free(lps);
    return -1;
}

// 定义一个函数，用于生成由n个c字符组成的字符串
char *repeat_char(char c, int n)
{
    // 分配n+1个字节的内存空间，用于存储字符串和结束符'\0'
    char *s = (char *)malloc(n + 1);
    // 判断内存分配是否成功
    if (s == NULL)
    {
        printf("内存分配失败\n");
        exit(1);
    }
    // 使用memset函数，将s的前n个字节都填充为c字符
    memset(s, c, n);
    // 在最后一个字节添加结束符'\0'
    s[n] = '\0';
    // 返回生成的字符串
    return s;
}

int main() {
    char* text = repeat_char('a', 1000001);
    text[1000000] = 'b';
    char* pattern = repeat_char('a', 101);
    pattern[100] = 'b';

    clock_t start_time = clock();
    int result = kmp_search(text, pattern);
    clock_t end_time = clock();
    double execution_time = ((double)(end_time - start_time)) / CLOCKS_PER_SEC * 1000.0;

    printf("Execution Time: %f ms\n", execution_time);

    if (result != -1) {
        printf("Pattern found at index %d\n", result);
    } else {
        printf("Pattern not found in the text\n");
    }

    return 0;
}


// output
// Execution Time: 8.270000 ms
// Pattern found at index 999900

测试用例：

1 2	`text = 'a' * 1000000 + 'b' pattern = 'a' * 100 + 'b'`

用时对比：

Algorithm	Time (ms)
Brute Force Search (Python)	10057.931
KMP Search (Python)	449.268
KMP Search (C)	8.270
Python find	1.748

可以看出 Python 和 C 的执行效率存在巨大差距。

6 引用

LeetCode 28. 找出字符串中第一个匹配项的下标 ↩

Algorithm > String > String Matching

#C/C++ #Python #LeetCode

字符串匹配之 KMP 算法

https://hwollin.github.io/2024/02/05/kmp/

作者

Wei Han

发布于

2024年2月5日

许可协议

二叉树的中序遍历上一篇

深入理解 CAS 下一篇

字符串匹配之 KMP 算法

1 问题描述[1]

2 Solution: Brute Force Search

3 Solution: KMP Algorithm

3.1 Basic idea

3.2 LPS 具体解释

3.3 算法预处理：为 pattern 构建 LPS 数组

3.4 搜索部分

4 效率对比

5 C语言版本KMP

6 引用

1 问题描述^[1]